FML Femag Modeling Language

FML erweitert die Skriptsprache FSL (FEMAG Script Language) um Befehle zur geometrischen Modellierung. Hierfür verwendet FML eigene Objekte (z.B. Punkte, Geraden, Kreise), die auf textueller Basis erzeugt und in Beziehung zueinander gesetzt werden. Die Verbindung zu FEMAG erfolgt über die Ausleitung von Punktkoordinaten aus den FML-Objekten. Diese Koordinaten dienen dem Anwender zur Knotenkettenerzeugung in FSL (mittels der Skriptbefehle nc_line, nc_circle etc.).

Da FML für die Verwendung mit einer Skriptsprache entwickelt wurde, weist es bestimmte Eigenschaften bzw. Konventionen auf, welche hinsichtlich des Verzichts auf direkte grafische Ein- und Ausgabemöglichkeiten von Bedeutung sind.

Typische Eigenschaften und Konventionen

Geraden

P1: erster Definitionspunkt der Geraden G1 P2: zweiter Definitionspunkt der Geraden G1

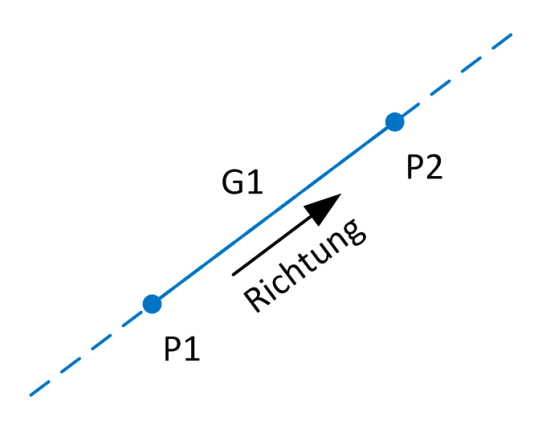
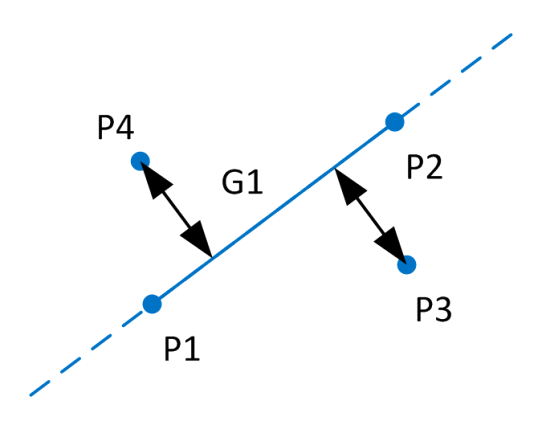
Geraden besitzen eine unendliche Länge und weisen eine Richtung auf. Dadurch ist es möglich, Objekte zu unterscheiden, die in “Fahrtrichtung” rechts oder links der Geraden liegen. Bei direkter Definition einer Geraden über zwei Punkte verläuft die Fahrtrichtung vom ersten angegebenen Punkt zum zweiten angegebenen Punkt. Die Definitionspunkte einer Geraden gelten nicht als deren charakteristische Merkmale, stattdessen wird intern eine Normalenform zur Darstellung verwendet.

Abstände

Abstände sind vorzeichenbehaftet.

P1: erster Definitionspunkt der Geraden G1 P2: zweiter Definitionspunkt der Geraden G1 Abstand (P3, G1) > 0, da auf rechter Seite in Fahrtrichtung von G1 Abstand (P4, G1) < 0, da auf linker Seite in Fahrtrichtung von G1

Schnittpunkte

Schnittpunkte besitzen eine Reihenfolge.

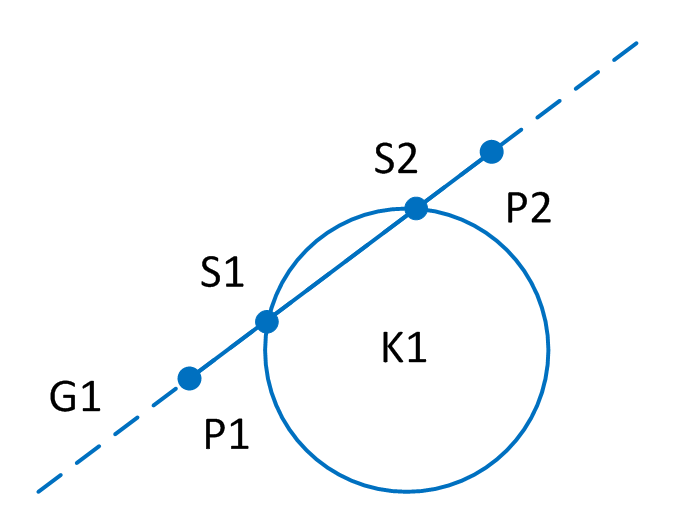
P1: erster Definitionspunkt der Geraden G1 P2: zweiter Definitionspunkt der Geraden G1 S1: erster Schnittpunkt von (G1, K1) in Fahrtrichtung von G1 S2: zweiter Schnittpunkt von (G1, K1) in Fahrtrichtung von G1

M1: Mittelpunkt des Kreises K1 M2: Mittelpunkt des Kreises K2 G1: gedachte Verbindungsgerade mit Richtung von M1 nach M2 S1: erster Schnittpunkt von (K1, K2), da auf rechter Seite in Fahrtrichtung v. G1 S2: zweiter Schnittpunkt von (K1, K2), da auf linker Seite in Fahrtrichtung v. G1

Tangentenpunkte

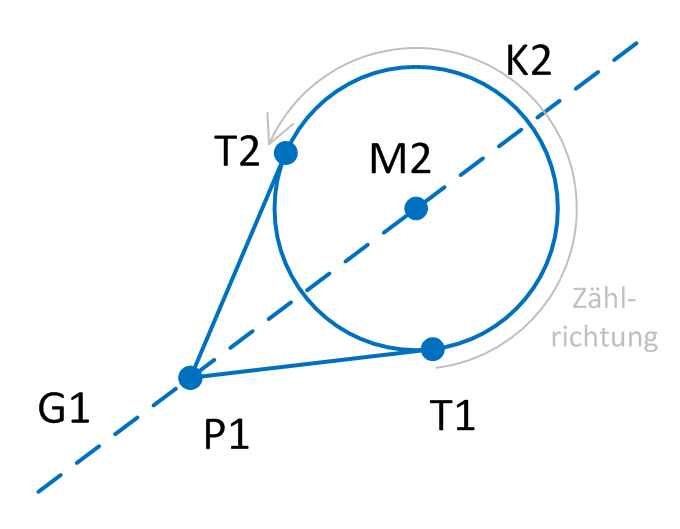
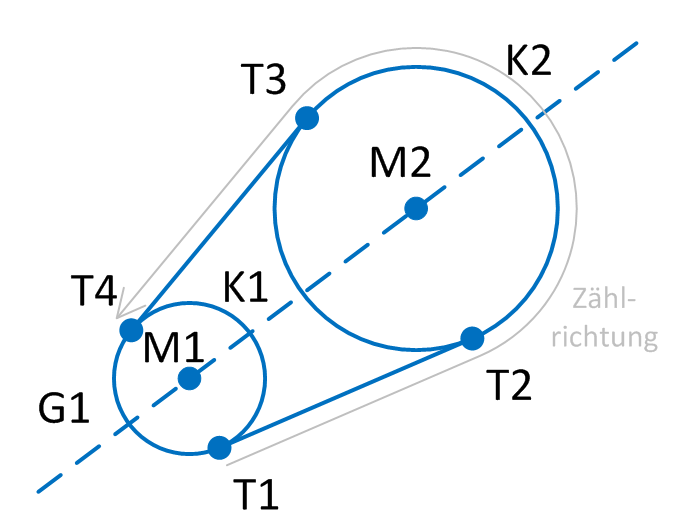
Tangentenpunkte besitzen eine Reihenfolge.

P1: erster Definitionspunkt der Geraden G1 P2: zweiter Definitionspunkt der Geraden G2 S1: erster Schnittpunkt von (G1, K1) in Fahrtrichtung von G1 S2: zweiter Schnittpunkt von (G1, K1) in Fahrtrichtung von G1

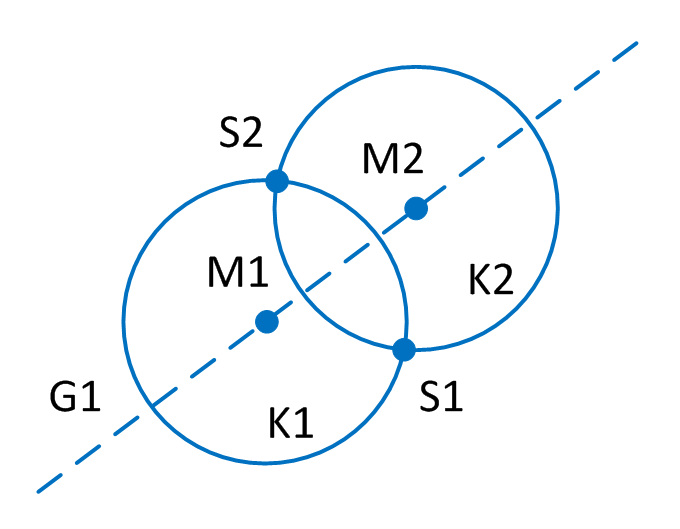
M1: Mittelpunkt von K1 M2: Mittelpunkt von K2 G1: gedachte Verbindungsgerade von M1 nach M2 T1: erster Tangentenpunkt von (K1, K2), da auf rechter Seite in Fahrtr. von G1 T2: zweiter Tangentenpunkt von (K1, K2) → weiter im GUZS T3: dritter Tangentenpunkt von (K1, K2) → weiter im GUZS T4: vierter Tangentenpunkt von (K1, K2) → weiter im GUZS

Reihenfolge der Funktionsparameter

Die Reihenfolge der an FML-Funktionen übergebenen Parameter (Argumente) spielt in der Regel keine Rolle. FML bestimmt die korrekte interne Verwendung anhand der übergebenen Objekttypen. Wenn jedoch bei Parametern gleichen Typs eine Information mit der Parameterreihenfolge verknüpft ist, werden die betreffenden Parameter in der nachfolgenden Funktionsbeschreibung mit Indizes versehen (z.B. point_1). Bei Vorhandensein dieser Indizes muss typweise auf die Parameterreihenfolge geachtet werden.

Mehrfachergebnisse

Sind mehrere Funktionsergebnisse möglich (z.B. zwei Schnittpunkte einer Geraden mit einem Kreis), müssen Indexparameter als Auswahlkriterium beim Funktionsaufruf verwendet werden. Ist “0” als Index zugelassen, werden sämtliche Ergebnisse in der Reihenfolge der Indexparameter zurückgegeben (Mehrfachzuweisung).

nil als Funktionsergebnis

Sofern ein Funktionsaufruf fehlschlägt, wird statt eines Objektes der Wert c{nil} zurückgegeben. Im Zweifelsfall sollte jedes neu erzeugte Objekt/Ergebnis hierauf geprüft werden.

Koordinatensysteme

FML verwendet zwei Koordinatensysteme: Ein globales Koordinatensystem, in dem alle Objekte angelegt werden und auf das sich alle Objekteigenschaften beziehen und ein optionales lokales Koordinatensystem, dessen translatorische und rotatorische Lage gegenüber dem globalen Koordinatensystem zur unmittelbaren Transformation der direkt vom Anwender eingegebenen Punkte dient.