Dakota Integration

Dakota <https://dakota.sandia.gov>_ is an open source toolkit (GPL License) for sensitivity analysis, uncertainty quantification, model calibration and optimization developped by Sandia National Laboratories.

Note

This module is in experimental state.

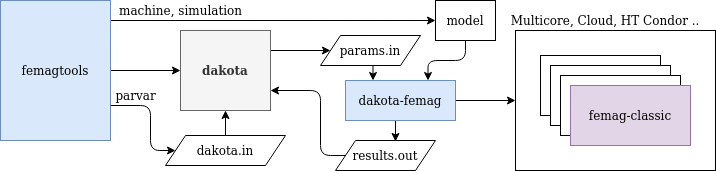
Example Parameter Study with Latin Hypercube Sampling:

machine = dict(
    name="PM 130",
    poles=4,
    ...
    stator=dict(
      num_slots=12,
      ..
      statorRotor3=dict(
        slot_width=3e-3,
        ... )  ),
    magnet=dict(
      ...
      magnetSector=dict(
        magn_shape=0.025,
        magn_width_pct=0.8,
        ... )  ),
    windings=dict(
      num_wires=20,
      .. )
)

parvar = {
  decision_vars = [
     {'bounds': [2e-3, 4e-3],
      'name': 'stator.statorRotor3.slot_width'},
     {'bounds': [0.75, 0.85],
      'name': 'magnet.magnetSector.magn_width_pct'},
     {'bounds': [0.021, 0.0335],
      'name': 'magnet.magnetSector.magn_shape'}
  ],
  objective_vars = [
    {'name': 'dqPar.torque[-1]', 'label': 'Load Torque/Nm'},
    {'name': 'torque[0].ripple', 'label': 'Cogging Torque/Nm'},
    {'name': 'torque[-1].ripple', 'label': 'Torque Ripple/Nm'}
  ]
}

simulation = dict(
  speed=5000.0 / 60,
  calculationMode="pm_sym_fast",
  magn_temp=20.0,
  wind_temp=60,
  period_frac=6,
  current=28.3,
  angl_i_up=0.0)

workdir = pathlib.Path.home() / 'parstudy'
workdir.mkdir(parents=True, exist_ok=True)

sampling = femagtools.dakota.Sampling(workdir,
             magnetizingCurves=magnetizingCurve, magnets=magnetMat)

# start calculation
results = sampling(parvar, machine, simulation,
                   samples=100, partitions=6,
                   engine=dict(module='femagtools.multiproc'))

Result: dict Object with keys:

x	array of decision (input) var values
f	array of objective (response) var values
samples
moments	mean, std dev, skewness, kurtosis
conf95	95% confidence intervals for each response
corr	correlation among all inputs and outputs
corrpartial	partial correlation between input and outputs
rank	rank correlation
opt	best inputs and outputs

Example:

x = results['x']
f = results['f']

# print header
print(' '.join(['{:15}'.format(s)
                for s in [d['label']
                          for d in parvar['decision_vars']] +
                [o['label']
                 for o in parvard['objective_vars']]]))
print()
# print values in table format
for l in np.vstack((x, f)).T:
    print(' '.join(['{:15.6f}'.format(y) for y in l]))